|
Table of contents:
1. PeterBURG
synopsis.
2. PeterBURG parameters:
tree intrface
nonterminals set
attributes data type
2. Grammar functor:
semantic
remantic
predicate
rule
module
Table
module
Labeler
module
Reducer
module
Verify
3. Additional functors
Synopsis
The PetersBURG logical structure is shown at the picture
below. In order to use BURS algorithm provided by PeterBURG
one need to supply three modules of certain module types.
First of all an interface to tree for rewriting needs to be
provided. This interface can be considered as a wrapper of the
actual tree representation. It seems any reasonable
tree-like data structure could easily be wrapped in such a
way and so be adapted for PeterBURG exploration.
In addition to tree interfaces to nonterminals
set and attributes data type must be supplied.
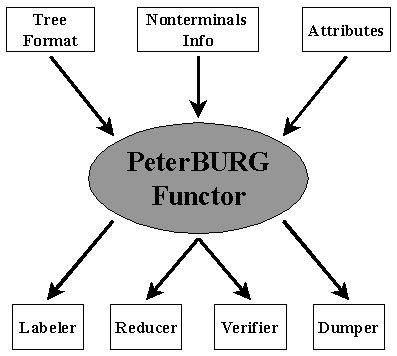
Being instantiated for modules described above PeterBURG
provides facilities for labeling and reducing of tree and
also for verification of the interfaces and
printing of intermediate data for debugging purposes.
Tree interface
Tree interface for PeterBURG is defined as module type Tree
and constists of the following entities:
type t - type of the tree
val terminals : int - number of
terminals. Terminals values must fit into interval 0..terminals-1
val degree : int - degree of the
tree
val term : t -> int - gets terminal label of
given node
val node : int -> t - shallow conversion from terminal to
tree node (for debugging purposes)
val sons : t -> t list - gets list of sons
from given node
val toString : t -> string - shallow
string representation
Nonterminals set
Nonterminals set interface must be provided by module of
module type Nonterminals consisting of two
items:
val number : int - number of nonterminals in BURS
grammar. Nonterminals values must fit into interval 0..number-1
val toString : int -> string - string
representation of given nonterminal
Attributes data type
Atribute is a value derived in tree node together with some
nonterminal. This value is calculated from given rule,
nonterminals labels of all sons of the node and their
attribute values. module type Attribute comprises
all needed entities:
type t - the type of attribute value
val cost : t -> int - the cost of the
attribute. This cost actually participates in dynamic
programming decision
val (<=) : t -> t -> int - ordering
function. This function can be used by PeterBURG to define
order of reductions during reduce stage (subtree with least
attribute value will be reduced first). a <= b returns 1 if
a < b, 0 if a = b and 1 if a > b. PeterBURG also provides
default function nosort to use when there is no need to control
order of reductions
val toString : t -> string - string
representation of attribute value
Grammar functor
Functor Grammar takes interfaces for tree (Tree),
nonterminals set (Nonterm) and attribute data type (Attr) and instantiates all BURS
functions for them.
Both nonterminals and terminals are treated as integers
inside Grammar module since appropriate functions provided
by Tree and Nonterminals interfaces.
type sema = Tree.t -> Attr.t
list -> Attr.t represents semantic action performed on tree
node and attributes of it's sons during labeling
stage.
type 'a rema = Tree.t ->
Attr.t -> 'a list -> 'a is the type of action performed over
tree node, it's attribute and result of reduce for all it's
sons during reduce stage. The polymorphic parameter 'a
represents type of value obtained as a result of reduce.
type predic = Tree.t ->
Attr.t list -> bool is the type of predicate that can guard
application of rule. The predicated rule can only be
applied when predicate being tested for tree node and
attributes of all it's sons returns true.
Two types provided by Grammar functor to denote BURS
rule. First of them - type 'a core - is actually the
rule comprising miscellaneous parts (deriving nonterminal,
tree node terminal, semantic actions for label and reduce
etc.) The second one - type 'a rule = 'a core *
string - is just the same structure decorated by string
label identifying rule for debugging purposes.
Several functions are provided to handle rules:
val rule : nonterm * Tree.t * nonterm
list * sema * 'a rema -> 'a core - creates non-predicated
rule. rule n t [n1; n2; ...; nk] lab red creates rule
deriving nonterminal n for tree node t with labeling
action lab and reducing action red when all sons of the
node have labeled with nonterminals n1, n2, ..., nk
correspondingly
val rule_p: nonterm * Tree.t * nonterm
list * predic * sema * 'a rema -> 'a core - the same, but
creates predicated rule
val chain : nonterm * nonterm * sema * 'a
rema -> 'a core - creates chain non-predicated rule
val chain_p: nonterm * nonterm * predic *
sema * 'a rema -> 'a core - creates chain predicated
rule
val toString: 'a rule -> string - converts
rule to readable format
module Table represents parsing table. This table
used to simplify matching of rules with the tree and
logically can be considered as two-dimensional table
indexed by node degree and terminal number.
Following entities are defined in the module:
type 'a t - type of the table
type 'a rc = Ok of 'a t | Fail of
string - type of return code of table build
function
val build: 'a rule list -> 'a rc -
function to build table from list of rules
val toString: 'a rc -> string - readable
representation for debugging purposes
module Labeler collects functions and types for
labeling stage of BURS process. There are:
exception Nomatch of Tree.t -
exception raised when no rule could be applied to node
passed with exception as a parameter
type 'a t - type representing labeling
result
type 'a rc = Ok of 'a t | Fail of string -
return code of labeling function
val toString : 'a rc -> string - debugging
function
val run : Tree.t -> 'a Table.rc -> 'a rc -
labeling function
module Reducer collects functions and types for
reduce stage of BURS process. There are:
type 'a rc = Ok of 'a t | Fail of string -
return code of reducing function
val toString : 'a rc -> string - debugging
function
val run : 'a Labeler.rc -> 'a rc -
reducing function
module Verify serves to verification of some guard
properties of modules provided as parameters. For example,
it checks that Tree.term (Tree.node i) = i for all i in
[0..Tree.terminals-1] etc. It is recommended to use
verification after first instantiation of functor for its
parameters to check consistency of interfaces. Verification
entities are:
type t = Yes | No of string -
result of verification
val run : unit -> t - verification
function
Additional functors
Two additional functors are provided besides
Grammar. First of all, functor BURS implements conventional
BURS e.g. dynamic programming without labeling
attributes. Then, functor ConstBURS implements BURS
without predicates and with constant costs.
Both of these functors are implemented as re-instantiations
of main Grammar functor and so have near the same interfaces.
|
